Every finite game has an equilibrium point (John Nash, Non-Cooperative Games, 1950)
I read recently this amazing book, where I discovered that we (humans) are not capable of generating random sequences of numbers by ourselves when we play lottery. John Haigh demonstrates this fact analyzing a sample of 282 raffles of 6/49 UK Lotto. Once I read this, I decided to prove if this disability is property only of British population or if it is shared with Spanish people as well. I am Spanish, so this experiment can bring painful results to myself, but here I come.
The Spanish equivalent of 6/40 UK Lotto is called “Lotería Primitiva” (or “Primitiva”, to abbreviate). This is a ticket of Primitiva lotto:

As you can see, one ticket gives the chance to do 8 bets. Each bet consists on 6 numbers between 1 and 49 to be chosen in a grid of 10 rows by 5 columns. People tend to choose separate numbers because we think that they are more likely to come up than combinations with some consecutive numbers. We think we have more chances to get rich choosing 4-12-23-25-31-43 rather than 3-17-18-19-32-33, for instance. To be honest, I should recognize I am one of these persons.
Primitiva lotto is managed by Sociedad Estatal Loterías y Apuestas del Estado, a public business entity belonging to the Spanish Ministry of Finance and Public Administrations. They know what people choose and they could do this experiment more exactly than me. They could analyze just human bets (those made by players by themselves) and discard machine ones (those made automatically by vending machines) but anyway it is possible to confirm the previous thesis with some public data.
I analysed 432 raffles of Primitiva carried out between 2011 and 2015; for each raffle I have this information:
- The six numbers that form the winning combination
- Total number of bets
- Number of bets which hit the six numbers (Observed Winners)
The idea is to compare observed winners of raffles with the expected number of them, estimated as follows:
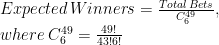
This table compare the number of expected and observed winners between raffles which contain consecutive and raffles which not:

There are 214 raffles without consecutive with 294 winners while the expected number of them was 219. In other words, a winner of a non-consecutive-raffle must share the prize with a 33% of some other person. On the other hand, the number of observed winners of a raffle with consecutive numbers 17% lower than the expected one. Simple and conclusive. Spanish are like British, at least in what concerns to this particular issue.
Let’s go further. I can do the same for any particular number. For example, there were 63 raffles containing number 45 in the winning combination and 57 (observed) winners, although 66 were expected. After doing this for every number, I can draw this plot, where I paint in blue those which ratio of observed winners between expected is lower than 0.9:

It seems that blue numbers are concentrated on the right side of the grid. Do we prefer small numbers rather than big ones? There are 15 primes between 1 and 49 (rate: 30%) but only 3 primes between blue numbers (rate: 23%). Are we attracted by primes?
Let’s combine both previous results. This table compares the number of expected and observed winners between raffles which contain consecutive and blues (at least one) and raffles which not:

Now, winning combinations with some consecutive and some blue numbers present 20% less of observed winners than expected. After this, which combination would you choose for your next bet? 27-35-36-41-44-45 or 2-6-13-15-26-28? I would choose the first one. Both of them have the same probability to come up, but probably you will become richer with the first one if it happens.
This is the code of this experiment. If someone need the dataset set to do their own experiments, feel free to ask me (you can find my email here):
library("xlsx")
library("sqldf")
library("Hmisc")
library("lubridate")
library("ggplot2")
library("extrafont")
library("googleVis")
windowsFonts(Garamond=windowsFont("Garamond"))
setwd("YOUR WORKING DIRECTORY HERE")
file = "SORTEOS_PRIMITIVA_2011_2015.xls"
data=read.xlsx(file, sheetName="ALL", colClasses=c("numeric", "Date", rep("numeric", 21)))
#Impute null values to zero
data$C1_EUROS=with(data, impute(C1_EUROS, 0))
data$CE_WINNERS=with(data, impute(CE_WINNERS, 0))
#Expected winners for each raffle
data$EXPECTED=data$BETS/(factorial(49)/(factorial(49-6)*factorial(6)))
#Consecutives indicator
data$DIFFMIN=apply(data[,3:8], 1, function (x) min(diff(sort(x))))
#Consecutives vs non-consecutives comparison
df1=sqldf("SELECT CASE WHEN DIFFMIN=1 THEN 'Yes' ELSE 'No' END AS CONS,
COUNT(*) AS RAFFLES,
SUM(EXPECTED) AS EXP_WINNERS,
SUM(CE_WINNERS+C1_WINNERS) AS OBS_WINNERS
FROM data GROUP BY CONS")
colnames(df1)=c("Contains consecutives?", "Number of raffles", "Expected Winners", "Observed Winners")
Table1=gvisTable(df1, formats=list('Expected Winners'='#,###'))
plot(Table1)
#Heat map of each number
results=data.frame(BALL=numeric(0), EXP_WINNER=numeric(0), OBS_WINNERS=numeric(0))
for (i in 1:49)
{
data$TF=apply(data[,3:8], 1, function (x) i %in% x + 0)
v=data.frame(BALL=i, sqldf("SELECT SUM(EXPECTED) AS EXP_WINNERS, SUM(CE_WINNERS+C1_WINNERS) AS OBS_WINNERS FROM data WHERE TF = 1"))
results=rbind(results, v)
}
results$ObsByExp=results$OBS_WINNERS/results$EXP_WINNERS
results$ROW=results$BALL%%10+1
results$COL=floor(results$BALL/10)+1
results$ObsByExp2=with(results, cut(ObsByExp, breaks=c(-Inf,.9,Inf), right = FALSE))
opt=theme(legend.position="none",
panel.background = element_blank(),
panel.grid = element_blank(),
axis.ticks=element_blank(),
axis.title=element_blank(),
axis.text =element_blank())
ggplot(results, aes(y=ROW, x=COL)) +
geom_tile(aes(fill = ObsByExp2), colour="gray85", lwd=2) +
geom_text(aes(family="Garamond"), label=results$BALL, color="gray10", size=12)+
scale_fill_manual(values = c("dodgerblue", "gray98"))+
scale_y_reverse()+opt
#Blue numbers
Bl=subset(results, ObsByExp2=="[-Inf,0.9)")[,1]
data$BLUES=apply(data[,3:8], 1, function (x) length(intersect(x,Bl)))
#Combination of consecutives and blues
df2=sqldf("SELECT CASE WHEN DIFFMIN=1 AND BLUES>0 THEN 'Yes' ELSE 'No' END AS IND,
COUNT(*) AS RAFFLES,
SUM(EXPECTED) AS EXP_WINNERS,
SUM(CE_WINNERS+C1_WINNERS) AS OBS_WINNERS
FROM data GROUP BY IND")
colnames(df2)=c("Contains consecutives and blues?", "Number of raffles", "Expected Winners", "Observed Winners")
Table2=gvisTable(df2, formats=list('Expected Winners'='#,###'))
plot(Table2)














