Tag Archives: strange attractor

Mandalaxies

Drawings, , , ,

One cannot escape the feeling that these mathematical formulas have an independent existence and an intelligence of their own, that they are wiser than we are, wiser even than their discoverers (Heinrich Hertz)

I love spending my time doing mathematics: transforming formulas into drawings, experimenting with paradoxes, learning new techniques … and R is a perfect tool for doing it. Maths are for me a the best way of escape and evasion from reality. At least, doing maths is a stylish way of wasting my time.

When I read something interesting, many times I feel the desire to try it by myself. That’s what happened to me when I discovered this fabolous book by Julien C. Sprott. I cannot stop doing images with the formulas that contains. Today I present you a mix of mandalas and galaxies that I called Mandalaxies:

This time, the equation that drives these drawings is this one:

x_{n+1}= 10a_1+(x_n+a_2sin(a_3y_n+a_4))cos(\alpha)+y_nsin(\alpha)\\ y_{n+1}= 10a_5-(x_n+a_2sin(a_3y_n+a_4))sin(\alpha)+y_nsin(\alpha)
where \alpha=2\pi/(13+10a_6)

The equation depends on six parameters (from a1 to a6). Searching randomly for values between -1.2 and 1.3 to each of them, you can generate an infinite number of beautiful images:

Here you can find the code to do your own images. Once again, Rcpp is key to generate the set of points to plot quickly since each of the previous plots contains 4 million points.

Rcpp, Camarón de la Isla and the Beauty of Maths

Drawings, , ,

Desde que te estoy queriendo
yo no sé lo que me pasa
cualquier vereda que tomo
siempre me lleva a tu casa
(Y mira que mira y mira, Camarón de la Isla)

The verses that head this post are taken from a song of Camarón de la Isla and illustrate very well what is a strange attractor in the real life. For non-Spanish speakers a translation is since I’m loving you, I don’t know what happens to me: any path I take, always ends at your house. If you don’t know who is Camarón de la Isla, hear his immense and immortal music.

I will not try to give here a formal definition of a strange attractor. Instead of doing it, I will try to describe them with my own words. A strange attractor can be defined with a system of equations (I don’t know if all strage attractors can be defined like this). These equations determine the trajectory of some initial point along a number of steps. The location of the point at step i, depends on the location of it at step i-1 so the trajectory is calculated sequentially. These are the equations that define the attractor of this experiment:

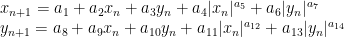
x_{n+1}= a_{1}+a_{2}x_{n}+a_{3}y_{n}+a_{4} |x_{n}|^{a_5}+a_{6} |y_{n}|^{a_7}\\ y_{n+1}= a_{8}+a_{9}x_{n}+a_{10}y_{n}+a_{11} |x_{n}|^{a_{12}}+a_{13} |y_{n}|^{a_{14}}

As you can see there are two equations, describing the location of each coordinate of the point (therefore it is located in a two dimensional space). These equations are impossible to resolve. In other words, you cannot know where will be the point after some iterations directly from its initial location. The adjective attractor comes from the fact of the trajectory of the point tends to be the same independently of its initial location.

Here you have more examples: folds, waterfalls, sand, smoke … images are really appealing:

The code of this experiment is here. You will find there a definition of parameters that produce a nice example image. Some comments:

  • Each point depends on the previous one, so iteration is mandatory; since each plot involves 10 million points, a very good option to do it efficiently is to use Rcpp, which allows you to iterate directly in C++.
  • Some points are quite isolated and far from the crowd of points. This is why I locate some breakpoints with quantile to remove tails. If not, the plot may be reduced to a big point.
  • The key to obtain a nice plot if to find out a good set of parameters (a1 to a14). I have my own method, wich involves the following steps: generate a random value for each between -4 and 4, simulate a mini attractor of only 2000 points and keep it if it doesn’t diverge (i.e. points don’t go to infinite), if x and y are not correlated at all and its kurtosis is bigger than a certain thresold. If the mini attractor overcome these filters, I keep its parameters and generate the big version with 10 million points.
  • I would have publish this method together with the code but I didn’t. Why? Because this may bring yourself to develop your own since mine one is not ideal. If you are interested in mine, let me know and I will give you more details. If you develop a good method by yourself and don’t mind to share it with me, let me know as well, please.

This post is inspired in this beautiful book from Julien Clinton Sprott. I would love to see your images.