Agarrada a mis costillas le cuelgan las piernas (Godzilla, Leiva)
Penrose tilings are amazing. Apart of the inner beauty of tesselations, they have two interesting properties: they are non-periodic (they lack any translational symmetry) and self-similar (any finite region appears an infinite number of times in the tiling). Both characteristics make them a kind of chaotical as well as ordered mathematical object that make them really appealing.
In this experiment I create Penrose tilings. Concretely, the P2 tiling, according to this article from Simon Tatham, that I will follow and provides a perfect explanation of how these tessellations can be constructed. The code is available here, and you can use it to create Penrose tilings like this one:

I will not explain in depth how to build the P2 tiling, since the article I mentioned before does it perfectly. Instead of that, I will give some highlights of the process together with a brief explanation of the code involved in it.
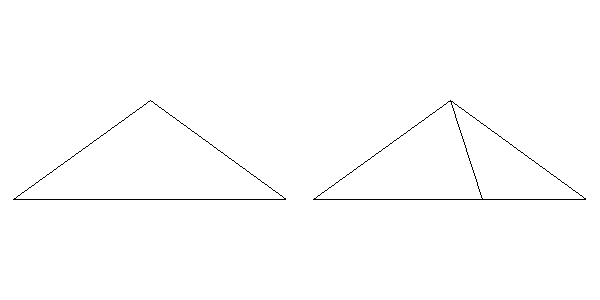
Everything has to do with triangles. Concretely, everything has to do with two types of triangles. To differenciate them I name their sides with numbers. The first triangle has labels 1, 2 and 3 and the other one has labels 1, 2 and 4. Two triangles of type 123 forms a kyte like this:

On the other hand, two triangles of type 124 forms a dart like this:

Actually, kites and darts don’t contain their inner segments so both of them are polygons of 4 sides. The building of a Penrose tiling is an iterative process that begins with 5 kites (i.e. 10 triangles of type 123) gathered like this:

You can start with many other patterns but this one will result in a round shape tiling and I like it. I build the tiling by subdividing triangles as Simon describes in his article. A triangle of type 123 is subdivided into three triangles: two of type 123 and one of type 124. The following image shows a 123 triangle (left) and the result after its division (right):

A triangle of type 124 is subdivided into two triangles: one of type 123 and one of type 124. The following image shows a 124 triangle (left) and the result after its division (right):
In each iteration, all triangles are subdivided according its type. After 5 iterations, the resulting pattern is like this:

To make calculations easier I arranged the data frame following a segment structure, in which the sides of triangles are defined by two coordinates: (x, y) and (xend, yend). The bad side of it is that I have rounding problems after making some iterations. It makes the points that would be the same differs slightly because they come from different triangles. I fix it using a hierarchical clustering and substituting points by its centroids after cutting up the dendogram using a very low thresold. Once this problem is solved I can remove the inner segments of all kites and darts, which are segments of type 3 or 4. Apart of removing them, I join the xx triengles to form 4-sides polygons. All these tasks are done with the function Arrange_df (remember that the code is here). This is the result:

This pattern is quite similar to its previous one but now the data frame is ready to be arranged as a polygon using the function Create_Polygon. At least, I calculate the area of each polygon with the Shoelace formula to create a columns called area which I use to fill polygons with two nice colors.
I hope that these explanations will help you to understand and improve the code as well as to invite you to create your own Penrose tilings.